机器学习

人工智能的三大基石技术之一

1. 推理
2. 知识
3. 学习

利用经验改善系统的性能

经典机器学习

学习是一个蕴含特定目的的知识获取过程，其内部表现为新知识的不断建立和修正，而外部表现则为性能改善

现代机器学习

任何通过数据训练的学习算法都属于机器学习

• 线性回归
• K-均值聚类
• 主成分分析
• 决策树和随机森林
• 支持向量机
• 人工神经网络

学习系统

stateDiagram
 模型空间 --> 学习算法
 数据 --> 学习算法
 学习算法 --> 学得模型

学习方法关系图

深度学习 < 表示学习 < 机器学习 < 人工智能

学习过程

分类和回归

常规术语及其标记

1. 输入 x, xi
2. 输出 y, y(x,W)
3. 权重 w, wi
4. 目标 t, tj
5. 误差 E

维数灾难

样本复杂度与输入X的维度直接相关

以同维度的立方体体积和球的体积做比，比是先增大后减小直到趋近于0

重要任务：对数据进行降维

数据集的划分

训练集、测试集、验证集

留出法、交叉验证

建模有关的要素

• 模型/映射函数的刻画(比如线性分类器,SVM,神经网络)
• 确定目标/损失函数(如平方损失，交叉熵，凸与非凸)并优化
• 评估

过拟合（Over-fitting）

极端追求样本上的误差减小，导致测试样本精度下降

欠拟合

学得不够

机器学习的共性问题

样本数是有限的，而满足这个样本的拟合函数/模型是大量甚至无穷的 –> 病态问题

模型选择

No Free Lunch Theorem 没有免费午餐定理

最好对问题有一些先验的知识

1. 模型选择
2. 正则化/规整化(给模型添加条件)
3. 模型组合或集成
4. 多视图方法

正则化可用

病态->良态

满足：

1. 存在性
2. 唯一性
3. ？

评价指标

混淆矩阵（多分类，二分类）

精度accuracy（预测对的数目占所有样本的数目）

错误率（1-精度）

查准率precision（查出来的正样本有哪些真的是正样本 tp/(tp+fp)）

查全率recall（所有的正样本有多少被查出来了 tp/(tp+fn)）

查准率和查准率会相互制约

F1度量： F1=2•(precision•recall)/(precision+recall)

ROC曲线

主要关注“真正是对的（查准率）”和“真正是错的”

不平衡数据集

正例数量和反例数量相差巨大

譬如普查艾滋病，如果模型无脑蒙阴性，正确率至少95%+，此时精度等指标往往不能很好地查出模型的问题

所以我们用Matthew系数进行不平衡数据集的度量

测量精度

系统的可重复性：类似的输入产生相近的输出

物理意义 类似于 概率分布中的方差

开发中往往愿意牺牲一些准确度选择测量精度更高的系统

先验的重要性

泛化=数据+知识

• 相似的样本应当有相似的输出
• 输入和输出间的映射应当光滑

丑小鸭定理

没有天生好的特征，只有结合了与问题相关知识的才是好的

统计学基本概念

数据集的统计量

均值、中位数、众数

期望：概率加权和方差、均方根

协方差cov

协方差矩阵

距离度量函数

计算样本和样本之间的距离

欧氏距离 距离公式

余弦相似性 比较余弦相似度

曼哈顿距离 总是沿着坐标轴走

切比雪夫距离 曼哈顿距离中长的那段

马氏距离 在新的空间上算距离

数据分布

高斯分布（正态分布）

概率

输入 男生女生 输出 身高

类的先验概率 p(y=i) 男生有70%

样本的先验概率 p(x) 175以下身高占40%

类条件概率（似然）p(x|y=i) 一个男生身高在175以下的概率

后验概率 p(y=i|x) 一个175的人是男生的概率

概率角度的机器学习方法分类

生成式模型

判别式模型

机器学习技术新发展

• 终身/连续学习
• 迁移学习和域适应
• 深度强化学习
• …

概率与学习：KNN

拿到数据之后，首先做一个特征工程（手动），得到比如一个特征向量

但是现在又有深度学习了，可以学习到数据的特征

分类问题

训练集

训练样本是这些x，它们一般是向量

样本标签是这些y，标签有时候是离散的，比如猫、狗，有时是连续的，比如身高

还要一个测试集来检验

回归问题

K近邻分类器

1. 计算样本和中所有训练样本之间的距离
2. 对计算的距离/相似度进行升序（降序）排列
3. 选择k个最近的训练样本
4. 采用投票法，将近邻样本数最多的类别标签分配给

最近邻分类器

• 泛化错误率：即便最近邻分类器如此简单，最近邻分类器的错误率没有超过贝叶斯分类器的两倍

k-近邻回归

将标签进行加和

更好的方式是离我越近的，我就给越大的权重，做加权平均：一种简单的方式是令权重为距离的倒数

近邻平滑

核平滑法

• 二次核
• 次方核
• 高斯核
• …

k-NN是典型的“懒惰学习”

• 训练阶段把样本存起来，啥也不做，所以训练开销为0
• 拿到了测试样本才真正开始计算
• 这在样本较小时是比较舒服的，但是如果样本很多就寄咯

SVM、CNN等是“急切学习”

训练阶段就对样本进行了学习处理，这类方法尝试在训练期间构造一个通用的、预输入无关的目标函数

KNN，评价

优点：

• 精度高
• 对异常值不敏感（把k设大点）
• 无数据输入假定

缺点：

• 计算复杂度高：
  • 训练阶段：0
  • 测试阶段：
    • logk是因为只用排出前k个，不用全拍了，所以不是快排的
• 空间复杂度高

降低计算难度

• 特征维度2-5：维诺图 Voronoi diagrams
  • 根据一组给定的目标，将平面划分成靠近每一个目标的多个区块
  • 维诺单元：X是一个点集，包含K个基点
    • 维诺单元永远是凸多边形
    • 不同的距离度量得到不同的维诺图
    • 查询或测试
      • 二维数据：计算图 查询
      • 多维可以做树优化，但是复杂度很难量化
• 特征维度6-30：KD-Tree
  • KD树是一种对K维空间中的实例点进行存储以便对其进行快速检索
  • 构造流程
    1. 确定split域，计算每个特征维度的方差，方差最大的维度即为split域的值
    2. 确定Node-data域，数据集点集按期第split域的值排序
    3. 。。。
  • 时间复杂度
    • 排序算法选得好的话
    • 查询：
• 高维特征：
  • 降维算法，例如PCA
  • 近似最近邻（approximate nearest neighbor，ANN）
    • 核心思想：搜索可能是近邻的数据项而不再只局限于返回最可能的数据项，在牺牲可接受范围内精度的情况下提高检索效率
  • 哈希（hashing）用简单的特征比如01代替复杂的特征比如实数
    • 利用hash将任意长度的输入映射为固定长度的输出

概率化KNN

传统knn的主要问题是不建立在任何概率框架上

K近邻算法的前途

小样本学习

无监督学习

聚类的好坏不存在绝对的标准

聚类也许是机器学习中“新算法”出现最多、最快的领域，总能找到一个新的“标准”，使以往算法对它无能为力

聚类算法

根据给定的相似性评价标准，将一个数据集合分组/划分成几个聚类（簇）

数学形式化

聚类的依据

将整个数据集中每个样本的特征向量看成是分布在特征空间中的一些点，点与点之间的距离可以作为相似度

一个好的聚类算法：

• 内部高相似性
• 之间低相似性

类的特征

• 不是实现给定的
• 聚类的数目和结构都没有实现假定

目的是寻找数据中的

• 潜在的自然分组结构
• 感兴趣的关系

距离度量对聚类的影响

数据的粗聚类是2类，细聚类是四类（因为距离度量函数不同）

数据分部形式影响聚类分析的有效性

距离度量

度量空间与度量函数

一个有序对,X是一个集合，d是X上的度量函数，d将X中的每一对点映射到一个非负实数，并满足一下四条公理

• 非负
• 唯一
• 对称
• 三角不等式
• 常用度量函数是前面讲到的一些距离，还有一个是把欧式、曼哈顿和切比雪夫距离囊括的闵可夫斯基距离（Minkowski distance）

聚类准则

• xi和xj之间的距离小于某个阈值就是一起的
• 试探方法
• 聚类准则函数方法

基于试探的聚类搜索算法

按最近邻规则的简单试探法

任取一个样本作为聚类中心的初始值，例如z1=x1

计算

如果小于阈值T，那么x2和z1在同一个聚类

如果大于，那么x2形成新的聚类中心z2=x1

接下来对于已经存在z1，z2…zn的情况，xn进来尝试归到小于阈值且最近的聚类中，如果都大于阈值，那么形成新的聚类

问题：

1. 样本初始选取产生不同分类
2. 样本顺序不同产生不同聚类
3. 阈值不同产生不同聚类

最大最小距离算法

基本思想：以试探类间欧式几何距离为最大作为预选出聚类中心的条件

1. 任意选一个样本作为第一个聚类中心z1=x1
2. 选距离z1最远的样本作为第二个聚类中心，比如z2=x6
3. 逐个计算剩下样本与z1，z2间的距离，并选出其中最小距离
4. 又选出最小值中的最大值，若改制达到z1-z2一定比例以上，那么取相应样本点为新的聚类中心

系统聚类法

基本思想：将样本数据按距离准则逐步分类，类别由多到少，直到获得合适的分类要求为止

聚类中心是一个由多到少的过程

1. 初始模式样本有n个，每个样本自成一类，即建立n类，计算各类之间的距离，得到一个初始矩阵
2. 假设前一步求得了距离矩阵，则求其中最小元素，如果是ij之间的距离，那么将两类合并为一类
3. 合并后计算新的距离
4. 返回第二步，重复计算及合并，直到达到满意的分类结果（比如聚类数量达到要求，或是最小距离超过了某个阈值）

距离准则函数

系统聚类法要计算聚类和聚类间的距离，这时就需要距离准则函数

• 最短距离法（两个集合间点距离的最小值）
• 最大距离法
• 类平均距离法

动态聚类法

基本思想：首先选择若干个样本点作为聚类中心，再按某种聚类准则（通常采用最小距离准则）使样本点向哥中心聚集，从而得到初始聚类

然后判断聚类是否合理，如果不合理则更改聚类

直到满意为止

K-means算法

1. 选择一个聚类数量k，这就是一个超参数
2. 初始化聚类中心
   1. 可以随机选
3. 对每个样本点，计算样本点到k个聚类中心的距离，将样本点分距离它最近的聚类中心所属的聚类
4. 重新计算聚类中心，聚类中心为属于这一个聚类的所有样本的均值
5. 如果没有发生样本所属的聚类发生改变的情况，则退出，否则，带着更新后的聚类中心返回step3

K-means算法的结构受到如下选择的影响

• 所选聚类的数目
• 聚类中心的初始分布
• 样本分布的几何性质

在实际应用中，需要试探不同的K值和选择不同的聚类中心的起始值

如果数据样本可以形成若干个相距较远的孤立的区域分布，一般都能得到较好的收敛效果

K-means++算法

基本思想：K个初始的聚类中心相互之间应该分得越开越好

1. 从数据集中随机选出一个样本作为初始聚类中心
2. 首先计算每个样本与当前已有聚类中心之间的最短距离（即与最近的一个聚类中心的距离），用;接着计算每个样本点被选为下一个聚类中心的概率$$。最后，按照轮盘算法择出下一个聚类中心
3. 重复第二步直到选出k个聚类中心
4. 然后就是k-means

ISODATA算法

运行过程中能够根据各个类别的实际情况进行分裂和合并两种操作来调整聚类中心函数

1. 从数据集中随机选取K0个样本作为初始蕨类中心
2. 针对数据集中每个样本xi，计算它到K0个聚类中心的距离并将其分到距离最小的聚类中心对应的类中
3. 判断上述每个类中的元素数目是否小于Nmin。如果小于Nmin则需要丢弃该类，令K=K-1，并将该类中的样本重新分配给剩下的类中距离最小的类
4. 针对每个类别重新计算其聚类中心
5. 如果类别数大于阈值，合并
6. 小于阈值，分裂
7. 直到达到迭代次数

合并操作：

1. 计算当前所有类别聚类中心两两之间的距离，用矩阵D表示，其中D(I，i)=0

2. 对于D(i,j)<dmin的两个类别需要进行合并操作，变成一个新的类，该类的聚类中心为：

   新的聚类中心可以看做是对这两个类别进行加权求和，如果一个类所包含的样本个数较多，所合成的新类就会更加偏向它

分裂操作：

1. 计算每个类别下所有样本在每个维度下的方差
2. 针对每个类别的所有方差调出最大的方差
3. 如果某个类别的>sigma并且该类别所包含的样本数量大于2nmin，那么认为可以分裂

与K-means算法的比较

• k-means算法通常更加适合于类别数目已知的聚类，而ISODATA算法则更加灵活
• 从算法角度看，ISODATA算法与K-means算法相似，聚类中心都是通过样本均值的迭代计算来决定的
• ISODATA加入了一些试探步骤，并且可以结合人机交互的结构，使其能利用中间结果所取得的经验更好的进行分类
• ISODATA原理非常直观，但是需要额外指定更多参数，在实际应用中并不受欢迎

聚类的评价指标

• 聚类中心之间的距离
• 聚类域中的样本数目
• 聚类域内样本的距离方差

常用评价指标（标签未知）

紧密度CP

是各个聚类样本点到聚类中心平均距离的平均值

间隔度SP

距离越大说明类间越分散

没有考虑到类内聚类效果

戴维森堡丁指数DBI

DB值越小，表示类内越紧凑，类间越分散

缺点：使用欧氏距离，对于环状分布聚类评价很差

邓恩指数DVI

计算任意两个簇元素最短距离除以任意簇内距离最大的值

聚类评价（标签已知）

监督学习与无监督学习

通过标注进行监督学习

但是标注实在是太麻烦了，人们开始寻找运用原始无标注数据的方式

自监督学习

• 自监督预训练
  • 无标签数据
  • 前置任务预训练
• 向下游迁移

前置任务学习

典型：生成式方法-图像着色

基本思想：如果一个模型有能力预测一张灰白图片的彩色状态，那么这个模型应该是可以识别这个物体的

• 彩色图像转为灰度图像，RGB->L（亮度）ab（色彩）
• L送给VGG，VGG网络重建ab
• 计算一个损失，损失如果在接受范围内就好噜

典型：图像修复

这个就比较难了

一幅图像去掉一部分，一段文章丢掉一些单词，要求模型补全

典型：图像拼图

把图像分成几个快，网络可以重新还原图像

对比学习

给图像做一些变换，并不改变其类别，网络应当可以发现他们是类似的

树学习

符号学习

推理

推理的角度

• 正向推理（演绎）
• 反向推理（反绎）
• 归纳推理

符号学习是一种归纳推理

概念学习

给定样例集合以及每个样例是否属于某个概念，自动的推断出该概念的一般定义

概念学习任务

• 实例集合X:上例中用六个属性表示
• 目标概念：定义在实例集上的布尔函数
• 训练样例：正例c(x)=1,反例c(x)=0
• 假设集：每个假设h表示X上定义的布尔函数

作为搜索的概念学习

当假设的表示确定后，也就确定了概念学习

假设的一般到特殊序

更泛化：

寻找极大特殊假设find-s

1. 将h初始化为H中最特殊的假设
2. 对每个正例x
   • 对h的每个属性约束ai
   • 如果x满足ai，不做任何处理
   • 否则将h中aj替换为x满足的另一个最一般的约束
3. 输出假设h

特点

对以属性合取式（&&的形式而不是||的形式）表示的假设空间，输出与正例一直的最特殊的假设

列表消除算法

变形空间

• 一致： h可以正确推断D
• 变型（版本空间）空间
  • 关于假设空间H和训练空间D能一致的所有h的集合
• 极大泛化
  • H中集合g和D一致并且不存在比g更泛化的g’还能与D一致
• 极大特化
  • H中集合s和D一致并且不存在比s更特化的s’还能与D一致

变型空间表示定理

候选消除算法

1. G初始化为最一般，S初始化为最特殊
2. if d是正例
   1. 从G中移去所有和d不一致的假设
   2. 对S中每一个与d不一致的假设s
      1. 从S中移除s
      2. 把s的所有极小泛化假设h加入到S中
         1. 且h满足与D一致，而且G中的某个成员比h更一般
      3. 从S中移去所有这样的假设：它比S中的另一假设更一般
3. if d是反例

归纳偏置问题

• 目标概念假设不在假设空间怎么办
• 能设计包含所有假设的假设空间吗
• 假设空间大小对未见实例的泛化能力有什么影响
• 假设空间大小对所需训练样例数量有什么影响

构造无偏的学习器

• 幂集
• 无偏学习的泛化
  • 给定3个正例q1,q2,q3,两个反例q4,q5

不同的归纳偏置

有偏程度不同的三种归纳学习算法

• 机械式学习器
• 候选消除算法
• FIND-S（只要和正例的统计结果不一致的都是大坏蛋）

有偏性

如果一个学习器的有偏性越强，那么它的归纳能力往往也越强

决策树学习

决策树学习

• 实例：“属性-值”对表示，应用最广的归纳推理算法之一
• 目标函数具有离散的输出值
• 有很好的健壮性（样例可以包含错误，也可以处理缺少属性值的实力）
• 能够学习析区表达式（析取是“或”，合取是“和”）

算法

• ID3，Assistant，C4.5
• 搜索一个完整表示的假设空间，表示为多个if-then规则（这使得模型具有一定的可解释性）

归纳偏置

• 优先选择较小的树

问题设置

问题设置

• 可能的实例集X
• 未知的目标函数f X->Y
• 得到一个函数集 H h:X->Y

决策树学习的假设空间搜索

• 搜索一个可以正确拟合训练样例的假设
• 搜索的假设空间就是可能的决策树的集合
• 从简单到复杂的爬山算法遍历假设空间

ID3算法

1. 创建树的root节点
2. 如果所有都为正，那就返回一个+的单节点root
3. 都为负，-
4. 如果属性都是空，那就返回一个root并且label标成example中出现最多的结果

否则（真的来了）

1. 选出A，A是属性中分类能力最好的属性
2. 根节点的决策属性就是A了
3. 对于A的每个可能值vi
   1. EVi为examples中满足A属性为vi的子集
   2. 如果ExampleVi为空，直接加一个叶子结点设一个最多的
   3. 否则，在这个分支下加一个子树，递归这个过程

核心问题：如何选择“最佳”或“最优”的属性

衡量给定属性区分样例的能力：信息增益

信息的度量：熵（这个样例集合的纯度，样本越是确定，越是一致，熵就越低，反之越高）

假设X是一个有限取值的离散随机变量：概率分布，随机变量的熵:

目标属性为布尔值的样例集S的熵

信息增益的计算：核心思想：使用某个属性分割样例后，样本熵下降的量，这个量越大，说明带来的信息增益就大

ID算法的特点

• 假设空间：包含所有的决策树
• 遍历过程：仅维持单一的当前假设
• 回溯：不进行回溯，可能进入局部最优
• 基于统计：对错误样例不敏感，不适合增量

决策树学习中的归纳偏置

1. 近似：优先选择较短的树
2. 优先选择信息增益高的属性更接近根节点的树

这是一种优先偏置（搜索偏置），而符号学习的算法一般都是限定性的，叫做限定偏置（语言偏置）

奥卡姆剃刀原理

如果对于同一现象有两种不同的假说，应该采取比较简单的哪一种（这样这个模型被证伪的机会就更少）

不是简单的选择最简化的假设，而是推理所依据的是使可证伪的假设的数目更少

C4.5算法

核心改进是属性选择指标

• 信息增益准则对可取值数目较多的属性有所偏好
• 信息增益比：信息增益/该属性的熵

CART算法

属性选择指标（分类）

Gini指数：对于模型纯度的刻画，越小越纯，也就越好

K个类，样本点属于第K类概率为pk

,而pk可以就用 该类样本数/总样本数 来近似

属性A对样本集合划分下的基尼指数

基尼系数 VS 信息增益

• 二分类问题
• 基尼系数和熵正相关，并且很接近，可近似代表分类误差率
• 都可以代表叶子结点的损失

CART算法还可以做回归问题

剪枝处理：增强模型的泛化能力

从完全生长的决策树的底端减去一些子树，使决策树变小，增强泛化能力

最小化子树损失函数

a是超参数，CT是预测误差，T是叶子数

决策树的优点

• 简单直观
• 可解释

缺点

• 非常容易过拟合
• 样本发生一点改动，树的结构可能剧烈改变

决策树的延伸

将决策树的可解释性延伸到深度学习网络

集成学习

核心思想：三个臭皮匠，顶个诸葛亮

是一个预测模型的元方法（并不是一个具体的学习方法）

特点（分类）

• 多个分类器集成在一起，以提高分类准确率
• 由训练数据构建基分类器，然后根据预测结果进行投票
• 集成学习本身不是一种分类器，而是分类器结合方法
• 通常集成分类器性能会好于单个分类器

数学保证

在精度互相独立的假设下，可以数学证明只要基分类器的精度优于随机选择，并且参考无穷多的分类器，集成分类器的精度可以趋于1

Bias-Variance tradeoff问题

• Bias 学习结果的期望与真实规律的差距
• Variance 学习结果自身的不确定性
• Total Error

当一个模型很简单，往往很难做到精确预测，但是结果会比较稳定，如果一个模型很复杂，相对预测（至少在测试集上）准确，但是结果会不稳定

核心问题

序列集成

• 利用基学习器之间的依赖关系，依次生成
• 减小偏差bias

并行集成

• 利用基学习器之间的独立关系，并行生成
• 减小方差variance

Core Problem

Q1：如何训练每个学习器

Q2：如何结合每个学习器

结合策略

回归问题

• 简单平均
• 加权平均

分类问题

• 各种投票

学习法

多样性策略

数据层面

• 输入样本的扰动
• 输出样本的扰动

属性层面

• 随机选择部分属性，构建基学习器

参数层面

Bagging原理

Bootstrap aggregating基本原理

• 有放回采样方法（数据层面）

  从样本池里面有放回的随机采样出多个不一样的数据集

流程

训练集S，基学习算法I，训练轮数T

for i = 1 to T:
	S' = 从S中采样
	Ci = I(S)
	
将Ci结果结合

Bagging的优点

• 并行式
  • 性能依赖基分类器
  • 不依赖训练集实例

缺点

• 基学习器拉胯，集成后也拉胯
• 集成后的模型缺乏可解释性
• 依赖数据集，计算代价还是比较高

代表算法：随机森林

• 用N来表示训练用例（样本）的个数，M表示特征数目，输入特征数目m，用于确定决策树上一个节点的决策结果（m远小于M）
• 从N个用例中以有放回抽样的方式，取样N次，形成一个训练集，并用未被抽到的作预测，评估其误差（数据扰动）
• 对于每一个节点，随机选择m个特征（通常为），根据这m个特征，计算最佳的分裂方式（属性扰动）
• 每棵树都会完整成长而不会剪枝，这有可能在建完一课正常树状分类器后会被采用

随机森林的特点

• 差异性：每棵树是不同的，每棵树使用的特征是不同的
• 缓解维度灾难：因为每棵树没有使用全部特征，特征空间被减小了
• 可并行化：不同数据，不同特征，每棵树都可以并行的生长
• 训练-测试划分：训练和测试的划分不是必须的，构建每棵决策树时，总是有30%的数据是没有采样的
• 稳定性：结果经过了投票和平均，比较稳定

Boosting与AdaBoost

概率近似正确理论（Probably approximately correct）

• 强可学习：如果存在一个多项式的学习算法能够学习到一个概念类，并且正确率很高，那么这个概念是强可学习的
• 弱可学习：多项式学不了
• 强学习器和弱学习器是等价的（并没有谁好或者谁差）
• 一个概念是
• 将弱可学习器通过boosting提升为强可学习器

框架

样本被分为简单样本和困难样本，本轮训练分类器可以正确处理的样本，被视为简单的样本，会被给予较低的权重，而无法正确分类的样本被视为困难样本，被赋予更高的权重，分类器带着分类的样本和权重进入下一轮迭代

Adaptive Boost

核心思想：

从弱学习算法开始，通过改变训练数据的概率分布（权值分布），反复学习，得到一些列弱分类器，然后进行组合，构成强分类器

策略：

• 权值分布
• 弱分类器组合：分类好的权重大，不好的权重小，组合

AdaBoost

训练样本集合

分类器样本权重

评估分类器

第k个分类器在训练集上的加权分类误差率为

权重系数

评估样本

样本权重

Adaboost理解

• 其实是一个加法模型

• 损失函数为指数函数

• 前向分步

Boosting Tree

加法模型，前向分步算法

以决策树为基函数的提升方法为提升树

采用平方误差损失函数

r是当前模型拟合数据的残差

拟合

梯度提升树GBDT

几乎没有听懂任何东西

初始化弱分类器，就用一个最小化弱分类器，都预测样本均值

​ 循环：

​ 根据残差构造样本集合

​ 构建CART树拟合刚刚构造的残差集合

​ 通过加法的方式，直接把刚刚拟合的结果加上去，直到达到循环退出的条件

得到强分类器

Extream Gradient Boosting（XGBoost）

在深度学习出现之前，XGBoost一直是Kaggle竞赛的首选方法

GBDT的高效实现

• 目标函数通过二阶泰勒展开式做近似
• 定义了树的复杂度
• 分裂节点处通过结构打分和分割损失动态生长
• 分裂节点的候选集合通过一种分布式

Stacking算法（学习法）

从初始数据集训练出

1. 对于Model_1，将训练集

比较

• Baggging：数据层面进行扰动
• Boosting：串行方法

概率与学习

黑话

• scalar 标量：一个实数

• vector 向量：一个实数序列构成一个向量

• matrix 矩阵：一个实数构成的矩形数组

• tensor 张量：一个泛化的实数构成的n维数组（0阶张量就是标量，1阶是向量，2阶是矩阵）

• 带约束的优化问题：

  minimizae f0(x)

  subject to

  • 优化变量：

• 不带约束的优化问题：注意现在我们说什么都是在说向量了

• 凸函数：X是一个凸集合

• 凹函数就是改下比较符号

• 判断函数的凹凸：对于标量函数，二阶导数大于等于0，是凸；对于向量函数，如果hessian矩阵是半正定的，则是凸函数

• 判断正定：特征值都大于等于0，都大于0就是正定

• 凹函数的判定又是反过来

• 随机变量的期望：取值对概率密度函数pdf积分（连续）或对概率质量函数pmf求和（离散）

• jensen不等式，如果是凸函数，那么凹反之

• 高斯分布：应用最广泛的概率分布

• 单变量高斯分布/正态分布（高中高斯分布）

  是平均数是标准差，方差越大，越矮胖，否则高瘦

• 多变量高斯分布

高斯混合模型 GMM

通过不同的权重，把不同的高斯模型组合在一起

概率密度函数也是加权求和的

可以将高斯混合模型数据的生成分成两个阶段来解释，首先生成了一个i，这个i决定了从第i个高斯分布中出现的，(一般i的概率就是高斯分布的权重)，然后再从第i个高斯分布中采样，这里i的生成我们就要假设有一个隐藏变量在决定它，也就是hidden z，我们可以认为，也就是z将会激活第i个高斯函数

那么既然z和x一一对应，那么怎么估计参数?

首先聚集每个子高斯分布的样本x得到

然后算出每个高斯模型的参数，权重就是 该模型的采样数/总采样数

最大似然估计 MLE Maximum likehood estimation

定义：MLE是通过最大化一个似然函数来估计一个概率分布的参数，使得在假设的统计模型下，观测数据最有可能出现

似然函数

最大似然估计MLE:

假设数据点i.i.d

高斯混合模型最大似然估计

最大对数似然估计MLE，同时还引入z

期望最大化算法 EM Expectation-Maximization algorithm

核心思想：一个迭代的方法，采用最大似然估计，先固定一个参数，然后去优化另一个，再固定这个，优化那个，一直迭代，直到局部最优

EM的实际运用完全没听懂

EM可以保证下界不断地被迭代与优化

Kmeans中就隐含着EM

点的类别就是隐藏变量，聚类中心就是参数，准则函数是让点们离聚类中心尽可能近

初始化就是一个选取预制参数的过程

E step是根据预选的中心，将点分到聚类

M step是根据点的类别，计算新的聚类中心

然后迭代

支持向量机

从统计学的观点来看，机器学习的目的是得到映射：

• 类的先验概率:
• 样本的先验概率:（样本中x的概率占多少）
• 类条件概率:(给定这个类别，它来自x的概率是多少)
• 后验概率:(我们最想要的，给定x，它是y的概率是多少？)

从概率框架的角度：

• 生成式模型
  • 估计和，用贝叶斯定理求
• 判别式模型
  • 直接估计后验概率
  • 判别函数：不假设概率模型，直接求一个把各类分开的边界

感知机：线性超平面

二分类问题

• 可以看做作是在特征空间上对类别进行划分的任务

如果可以找到一个超平面可以让$\mathbf{w^T x_i}+b0$时将数据i分成不同的类别，那么这就是一个可以用线性超平面解决的二分类问题

而我们在机器学习中要求的就是和

线性支持向量机

核心思想：最大化所有训练样本的最小间隔

• 计算所有样本点到想象中的超平面的间隔
• 找到那个最小的间隔
• 我们希望这个间隔最大化

支持向量

具有最小间隔的样本点被叫做支持向量

样本点到超平面的距离

看起来就是高中点到直线距离的展开

证明与高中也相似

SVM问题是什么？

找到一组w，b，使得对于所有样本的至超平面的最小间隔最大

如何简化计算？

我们可以对于w,b乘以一个参数c得到cw，cb，而这两个数也可以实现分类，就好像把超平面沿着它延展的方向移动了一样

于是我们找到一个合适的c，使得

可以让c为最优解的最小间隔，这样同时一除，就相当于限定为1，于是我们就只需要最大化

于是我们进一步转为求解最小，使得

接下来我们将带约束的优化问题转为不带约束的优化问题

拉格朗日乘子法

SVM对偶形式

原来，变量是，拉格朗日之后，变量是

求出现在的最优解，就能得到原空间的最优解

求出了w*，怎么求b*呢

对于拉格朗日乘子>0的情况，就一定有

优化与改进

不能给予过强的假设，我们应该允许少数点不满足

可以允许少数点margin比1小

但是犯错误要有惩罚

我们做了一个松弛

为了避免非常离谱的，我们必须做一个惩罚

让优化目标成为

代价

正则项

C超参数

很多样本是不可以通过线性超平面分类的，很可能是非线性

把数据映射到高维空间

定理：如果原始空间是有限维（属性数有限），那么一定存在一个高维特征空间使样本可分

核技巧：

定理：低维度空间的非线性函数，我们可以找到一个高维（尽管可能是无限为），将它转为高维空间里向量的内积

核支持向量机kernel SVM

将对偶形式的xi,yi内积替换为核函数，对应的分类边界中xi也成为$$

常用的kernel function

现实中的分类往往也不是二分类，对于多分类我们该怎么做呢

如何选择超参数呢

采用交叉验证的方式

如何解决多类问题呢？

• 最原始的方式：每两个类之间都训练出一个分类器
• 另一种：设计C个分类器，对于类别i，除了i以外的类别都是负类

神经网络来了！

神经元和感知机

发展历史

• 1943 一个心理学家和一个数理逻辑学家提出
• 1948 冯诺依曼提出相互再生自动机网络
• 1950s 感知机模式
• 1960s 非线性多层自适应网络
• 1969 《感知机》
• 1982、1984 Hopfield
• 2006 深度信念网络

MP神经元基本结构

• 输入X
• 权值W
• 激活函数
• 偏置单元,对应权值

一组输入加权wi相当于突触

一个加法器把输入信号相加，与收集电荷的细胞膜相似

一个激活函数决定神经元是否要被激活，类似细胞是否放店

MP神经元的局限

输入方面：线性求和

输出方面：单一输出值

更新机制：时钟同步更新

• 权值的物理意义：兴奋、抑制

激活函数

单个神经元不管怎么样都是在求和，怎么搞都是线性操作

激活函数就引入了非线性

阶跃函数

• 不连续
• 对变化敏感
• x=0 时不可微
• 适用于单层感知机

sigmoid函数

阶跃函数的平滑近似

• 连续、光滑、严格单调
• 函数范围在(0,1)之间
• S形曲线，非线性函数
• 导数为其本身函数的组合

问题：

• 饱和性激励函数（当趋于无穷时梯度趋于0）
• 梯度和导数很容易变成0，导致梯度消失
• 导数始终小于1，在0周围变化
• 不以0为对称轴
• 指数计算代价大

ReLU

Leaky ReLU(a=0.01)/PReLu

RReLU

在训练时a从一个均匀分布中采样

最早的神经网络

ALVINN

感知机与感知机学习

最简单形式的前馈式神经网络

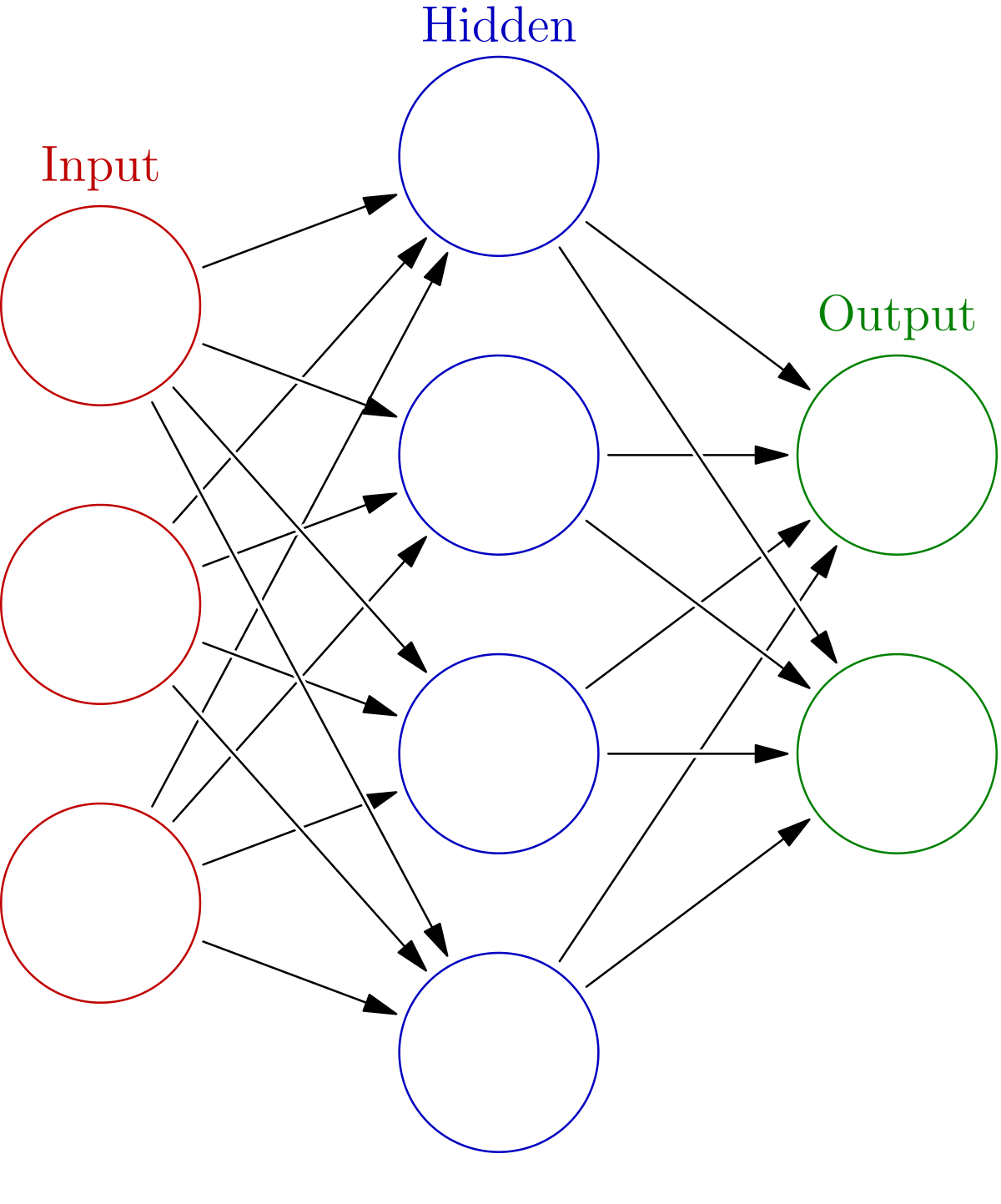
input是输入，hiden是隐藏层，是神经元的主体，边上有权重，最后输出前走一次激活函数

非线性前馈网络

• 同层内无互联
• 层层间全相连

有监督学习机制

每一轮我们会计算一个权值的变化量

感知机学习算法

1. 初始化权值
2. 计算权值和，应用激活函数，获得输出
3. 查看输出和期望是否一样，如果不一样就会更新权重

线性可分

决策边界

• 鉴别函数

感知机收敛理论

给定一个线性可分数据集，感知机将在有限迭代中收敛到一个决策边界

定义是分离超平面与最接近的数据点之间的距离，则迭代次数的界是

感知机学习缺点

• 感知机属于单层神经网络，不能解决非线性可分问题
• 典型的例子是异或
• 一种方法是投影到高维空间
• 也可以采用多层感知机，就好像对数据进行了变换，可以在影藏层做升维，也可以增加神经元相当于变换数据
• 感知机的表达能力

走向远处

多层感知机MLP

为什么要有隐藏层？

隐藏层实际上是特征检测算子，隐藏层神经元逐步发现数据的突出特征

如何计算隐藏层的权值？

前向与后向

前：分阶段，逐层计算，逐层输出

后：计算一个偏差，分阶段，逐层调整权值

反向传播

误差反传

误差的计算

Delta规则

Delta规则是基于错误平面的（神经网络在训练集上的累积误差，每一个权值向量都会对应一个误差，也就对应误差平面上的一个点），Delta规则要求激活函数连续且可微分

学习常数C对于delta规则影响很大，c过小更新很慢，c过大会在最优震荡

反向传播算法

• 前向阶段：网络权值固定，输入信号在网络正向一层一层传播，直到达到输出端，获得网络的输出
• 反向阶段：通过比较网络的输出与期望输出，产生一个误差信号，误差信号通过网络反向一层一层传播，在传播过程中对突触的权值进行修正
• 信用分配问题：修正隐藏值的权值时，如何给隐藏层的神经元分配信用或责任呢

BP神经网络：

• 三层或三层以上结构
• 无反馈
• 层内无连接
• 输入层+输出层+隐含层
• 采用误差反向传播学习算法

BP本质上是一个学习算法，MLP假借了它的名字成为BP学习算法

• 神经元是输出层可以直接用真实值算误差
• 但是隐藏层没有期望输出，所以要借助下一个节点的误差传播来实现

随机梯度下降

• 最小化一个损失函数

• 批量梯度下降：拿全部的样本去算梯度，取平均值更新

• 只拿一个样本去更新肯定也不行吧（随机梯度下降）

• Mini-batch随机梯度下降：随便搞一些来更新

反向传播就是利用链式法则，根据下一层的偏导数*本层的输出对于本层的权值的偏导数，乘上学习因子就是了

初始权值

简易方法是权值直接服从正态分布（0,1），但是权值过大会导致sigmoid饱和，导致梯度趋近于0，进而导致学习失效，所以早期我们使用（1，1/√n）

批量训练

今天，20世纪的人们爱用mini-batch

局部极小和冲量

冲量相当于加大步长，借此跨过一些局部最优

停止机制

• 固定迭代步数
• 误差小于某个阈值直接停下来
• 利用验证集观察误差的变化，打击过拟合

自动编码器 AutoEncoder

早期的自动编码器用来去噪

Encoder->latenet space -> Decoder

自动编码器可以实现无监督的特征提取，也可以在latenet space进行采样丢给decoder生成新的数据

径向基网络RBF

受到视网膜的启发，RBF认为不需要每个神经元都接受全部的信息，而是可以接受一部分，也即感受野

高斯函数作为激活函数

当神经元的输入离径向基函数越近，神经元激活程度越高

…越远…程度越低

输入空间到隐层空间是非线形变换

隐层空间到输出空间是线性变换

求解的参数

1. 基函数中心、方差
2. 隐藏层到输出层的权值

径向基函数算法

• 放置RBF中心
  • 用均值算法初始化RBF中心的位置
  • 用随机选择的数据点作为RBF的中心

BP是对非线形映射的全局逼近，可以有多个隐层

RBF具有局部映射的特性，只存在一个隐含层，RBF计算速度快

深度学习

经典机器学习

input->特征表示->学习算法

深度学习

神经网络自动学习特征

深度学习具有良好的非线形结构

神经网络可以一层一层的拆分十分复杂的复合函数

手工特征

• 固定
• 难以设计
• 任务无关
• 底层特征
• 需要专业知识
• 与学习算法是分离的

深度特征

• 特征是可学习的
• 黑盒
• 学到的特征与任务是相关的
• 学习层次表示和高级特征
• 端到端的，特征抽取与学习算法耦合在一起

卷积神经网络

局部连接的神经网络

对于一个1000*1000的图片，如果隐藏层也是1000*1000，如果还是全连接，最保守估计也有10^12个参数

所以我们使用局部连接，如果我们使用10*10的局部连接，我们就只需要10^8个参数了

但是这样还是很离谱，于是有人提出了“参数共享”的机制，比如就只要100个Filter（滤波器），每个Filter自己有一组参数，就只有100*100=10000个参数了

卷积核

卷积

池化Pooling/下采样Subsampling

• 减少参数
• 避免过拟合
• 扩大感受域（池化后单个点对应的上一层的区域要大得多）

因为中间神经元可能会很大，给下一层带来很大的压力，因此我们可以采用池化减小中间神经元

• Max pooling
• Average pooling
• L2-norm pooling
• Global average pooling
• Covariance pooling
• …

最后如何对应到输出呢？

把最后一层输出拉成一维向量，交给全连接神经网络，最后得到一个输出向量，比如十分类问题，我们就可以得到一个十维向量

但是这样不就又陷入了全连接巨大的参数陷阱么？

所以我们可以通过Global Average Pooling，先进一步大幅减少参数量，在去映射到解空间

Dropout

解决全连接巨量参数的问题，我们可以直接抛弃一些连接，这就好像人类从儿童变为成年人时大脑的神经元连接数在不断的减少一样

最简单地Dropout以固定的概率p随机保留一写神经元，这意味着每次Dropout，神经网络都是不一样的，从这个角度来讲，也是一种集成学习

因为Dropout可以带来非常可观的性能提升，现在大家不仅对全连接层做Dropout，还对卷积层有时也Dropout

Batch Normalization

通过对每层的输出进行归一化，我们可以减少内部方差偏移或避免梯度扩散

BN可以帮助我们把网络搭得更深

BN首先对每层的结果做了减去平均数和除以方差的操作，然后为了避免破坏结构又反过来做了类似的事

交叉熵损失函数

• 将错误类别的负对数概率降至最低
• 最大化真实类别的正对数

回归损失函数

回归问题的label是连续值，需要拟合真实标签的值

三元组损失

三元组损失比较锚点和结果的相似度1

机器学习技巧

数据增广

比如flipping（翻转），crop（裁剪）、color jitter;ing（颜色变化）

除了可以增加数据量，还可以提高模型的泛化能力

mixup（图像按不同权重拼接起来）

cutmix（把一个目标裁剪下来帖到另一个上）

预处理

过滤器

batch-size 每次训练采用的样本数，比如数据集有1000张，每次只用100张，batch-size能选多大和gpu的能力直接相关，因为要把样本载入显存

filter-size也会对结果产生效果

池化大小

学习率的设定（重中之重）

学习率的效果与优化器也有关

SGD是随机梯度下降最经典的优化器

Adam优化器是SGD的优化成果

SGD类开始可以采用比较大的学习率，然后随着迭代将学习率降得越来越小

adam优化器一般就采用一个固定的学习率

当batch-size很大时，可以采用比较大的学习率，如果比较小就要更谨慎一点

预训练

避免模型随机初始化，比如预训练的大模型可以快速帮助我们训练出具体的好的大模型

在预训练模型上微调时不要一下子调所有的参数，而是调一小部分或是新嫁接一些层数

但是如果你手里数据量很多，就不用束手束脚，直接微调大量参数甚至整个模型都没事，如果是新加一层的话，新加的层学习率可以设大点，原来的层学习率可以设小点，如果是指更新部分参数的话（很多参数里面都有requireGraddiance这个选项，为false时神经元就不会接受梯度带来的更新了）

激活函数的选择

图像分析

tensorboard可以画出一些关键的数据比如损失随着训练轮次的变化

当验证集上的精度和训练集上的精度差别很大时，模型应该是过拟合了

还可以把一些重要的特征可视化

注意力机制

经典神经网络架构

LeNet

第一个成功的神经网络，识别支票的数据

AlexNet

leNet风格的骨干网

VGG

ResNet：目前最成功的网络

提出了残差的结构，可以帮助实现数百甚至上千层的网络

Vision Transformer

RNN

把上一时刻的输出当成下一时刻的输入

LSTM长短期记忆网络

通过输入门和遗忘门控制信息流

Self-Attenton

演化学习

涌现学习模型：模仿生物的生命演化形式

遗传算法：学习是问题候选假设（解）在进化中的一种竞争，较好的候选假设在自然选择中不断演化

人工生命：模拟生物的进化条件

• 在连续的世代中有选择地淘汰适应性较低的个体，通过这样简单的过程，生物体的适应性得到提高
• 演化和涌现出现在群体中
• 选择的压力不仅来自外部环境，也来自群体中个体相互作用中

遗传算法 genetic algorithms（GA）

通过对当前最好的假设模型重组来产生后续假设模型

生成并测试的柱状搜索

一般形式

1. t:=0，初始化种群P(t)
2. 如果不满足终止条件
   1. 评估种群P(t)中每个染色体的适应度
   2. 根据适应度函数选择部分染色体
   3. 根据所选择的染色体产生后代
   4. 根据P(t)中染色体的适应度，选择被替换的染色体，以后代替换
   5. t:=t+1
3. 终止

如何表示染色体？

二进制位串的编码

每个属性值用二进制的1位表示

单属性

100 sunny

110 sunny||overcast

111 sunny || overcast || rain

多属性合取

101 10 (sunny||rain)&strong

if then规则

101 10 10

决策属性

用一位表示

1(Yes)、0(No)、#(Don’t care)

什么是适应度函数？

示例

背包问题，假设背包容量为50

1代表选择相应的物品，0代表不选

适应函数目的是找更高的值集合

fit(染色体)=所有物品的货币价值和，当总重量大于50时设为0

种群是一组染色体及其计算的适应度

GA工作在每一代的种群上，第0代种群中染色体随机生成

如何选择染色体？

选择父母

锦标赛选择：每次从种群中取出一定数量的个体，然后选择其中最好的一个M进入子代种群，重复该操作，直到新的种群规模达到原来的种群规模

截断选择：根据适应度排序，前f个染色体进入下一代种群，对染色体进行复制，直到填充至种群规模达到原来的种群规模

轮盘赌选择：与适应度成比例选择 当前适应度/总适应度，还可以利用指数函数全算成正值

注意探索和利用的平衡

如何产生后代？

遗传算子：对当前群体中选择的染色体进行重组，以产生后代

交叉：选择两个候选个体，分解每一个个体，然后交换分量形成两个新的候选个体

• 单点交叉
• 两点交叉
• 均匀交叉

变异：选择一个候选个体，随机的选择一位，然后取反

常以小概率1/L（L是染色体长度）发生变异

后代种群演化

简单方法：直接替代父代染色体：易丢失优秀解

精英法：替换掉最差的

锦标赛法

小生境法：将每一代个体划分为若干类，每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个群，再在种群中，以及不同种群之间杂交，变异产生新一代个体群

GA的优势

• 无需理解问题内部的相关性和因果性
• 以一个随机群体开始，以适应度作为某种启发式
• 进化论保证整个种群的演化

未解决的问题

• 表示的问题：编码不规范，表示可能也不准确
• 约束的问题：单一的遗传算法编码不能全面地将优化问题的约束表示出来，考虑约束的一个方法就是对不可行解采用阈值，这样计算的时间必然增加
• 搜索效率问题：一般比其他算法慢
• 过早收敛：遗传算法容易过早收敛

模式

m(s,t)表示在第t代种群pt中模式s的实例数量

自然计算

• 模仿自然界特点
• 具有自适应、自组织、自学习能力的模型与算法
• 遗传算法、蚁群算法、粒子群算法、免疫算法
• 往往用来解决非凸优化的问题（凸优化可以直接用梯度找到最优解）

学习分类器系统

维度约简

• 特征选择
• 特征诱导/变化

目的：

• 降低过拟合风险
• 避免维度灾难
• 增加可解释性
• 去除冗余特征

我们很难想象在高维空间中数据之间有什么关系

特征选择

N个原始特征，2^N-1非空特征空间，搜索最优的特征子集

搜索方向

前向（起点为空），后向（起点为全集），双向

搜索策略

穷举、序列、随机

特征评估函数（用于判断特征是否重要）

过滤式、封装式

过滤式

• 使用评价准则来增强特征与类的相关性，削减特征之间的相关性
• 距离度量、信息度量、依赖性度量、一致性度量

封装式

• 特征及其与任务目标的相关性
• 如分类错误率

嵌入式

模型正则化，如加上稀疏约束

线性判别分析LDA

1. 计算每个类别的均值,全局样本均值
2. 计算类内散度矩阵Sw，类间散度矩阵Sb
3. 对矩阵Sw-1Sb做特征值分解
4. 取最大的数个特征值所对应的特征向量
5. 计算投影矩阵

主成分分析PCA

无监督特征降维方法

找到数据中的主要成分，并以之表征数据

最大可分性：样本点在第一主成分上的投影其离散程度要大于其在第二主成分上的投影的离散程度

最近可重构性：样本点到第二主成分的平均距离都要大于其到第一主成分线的距离

最大化样本点在主成分上投影的偏差

1. 给定去中心化的样本数据（方便算协方差）
2. 投影后数据
3. 计算投影后数据的方差
4. 最大化投影数据方法 max tr(WtCW) 前提：WtW=I

求解优化目标函数：拉格朗日乘子法

独立成分分析

因素分析FA

假设数据是由多个数据源产生的，并且有噪声，我们想将数据解释成少数不相关因素的叠加

独立成分分析

期末

第一章-概论

各种概念的了解

第二章-聚类

• 距离度量函数
• knn流程
• 超参数的意义
• 减少计算复杂度

第三章-无监督学习

• 聚类准则
• 聚类评判
• 三类聚类方法中比较有代表性的：基于试探、系统聚类、动态聚类、常用的评价指标（前沿进展不考咯）

第四章-树学习

• 概念学习
• 怎么构造决策树，怎么选择节点 id3
• c4.5 cart各种不同的评价指标

第五章-集成学习

• 集成学习基本原理
• bias-variance tradeoff
• bagging boosting
• adaboost、GBDT、XGBoost看一看就行

第六章-概率与学习

• 高斯混合模型
• 带约束优化、不带约束优化（比如最小二乘）
• 最大似然估计、期望最大化（核心思想要了解）

第七张-支持向量机

• 都要看

• 推导不会现场要求

• 非线性支持向量机

第八章-神经元与感知机

• 脑和神经元
• 感知机学习
• 线性可分
• 激活函数

第九章-神经网络

• 更深入的要求
• 多层感知机 损失、前向传播、反向传播

第十章-卷积网络

• 卷积
• 核心概念、关键模块

第十一章-演化学习

• 遗传算法
• 模式理论

第十二章-维度约减

• 线性判别分析
• 主成分分析
• 独立成分分析

第十三章-强化学习

• MPD模型
• 动态规划
• 强化学习
• 蒙特卡罗方法
• 时间差分方法
• 自举方法、采样
• Q学习、TD、回退