教材link

复数 (Complex Number ) 与矩阵旋转

四元数和复数有非常大的相似度

复数的常见运算可以等价为矩阵的常见运算

任何一个复数可以表示为矩阵

其相应的加法与乘法都可以等价过来

我们知道二维旋转矩阵的公式是

这个矩阵也可以被表示成一个复数，即

那么这时向量也表示成

旋转过程即被表示为

极坐标与复数

欧拉公式

之前完全就是只听说过名字

对任意实数x，都存在

另x=，得到欧拉恒等式

证明可以使用我们的好朋友泰勒公式，对泰勒展开即可将奇数项和偶数项分别凑出cosx和sinx的泰勒展开式

欧拉公式给出了复平面中对圆的描述

所以我们可以将复数改写为

其中是模长，是xy通过atan2给出的方向角

如此复数就可以被一个缩放因子r和旋转角定义

旋转公式也就被表示为

由于复数乘法满足交换律，因此旋转是可以复合操作的

三维空间的旋转

假设我们有一个穿过原点的旋转轴为，现在我们要旋转向量

（如果实际操作中旋转轴不穿过原点，可以先把旋转轴移动到原点，转完再移回去，这就是MVP变换的思想之一了）

任何要对着这个轴旋转的向量都可以被分解到两个方向——垂直方向和平行方向

平行u方向什么都不用做，垂直u方向可以被降维为2D平面中的旋转

2D平面的基向量由在这个2D平面的分量和这个分量与的叉乘给出

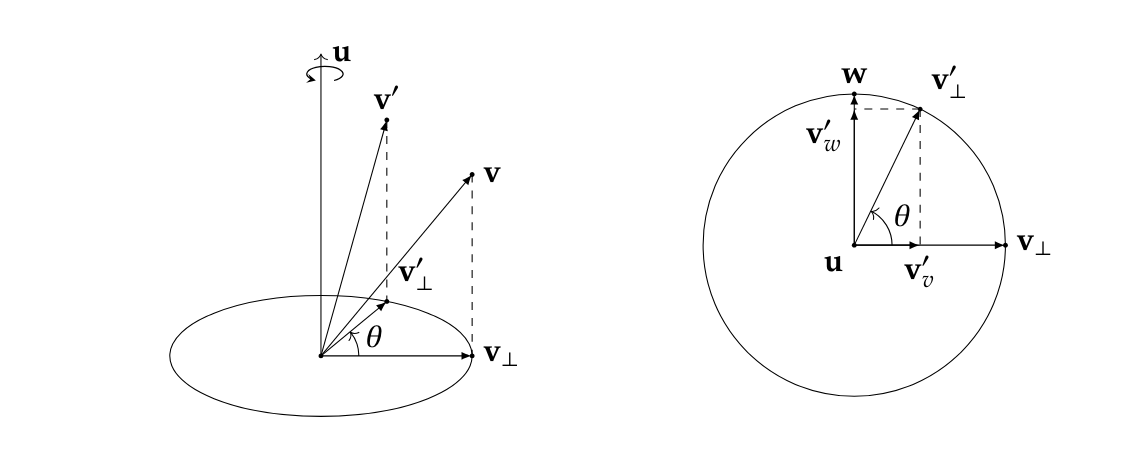
从而有

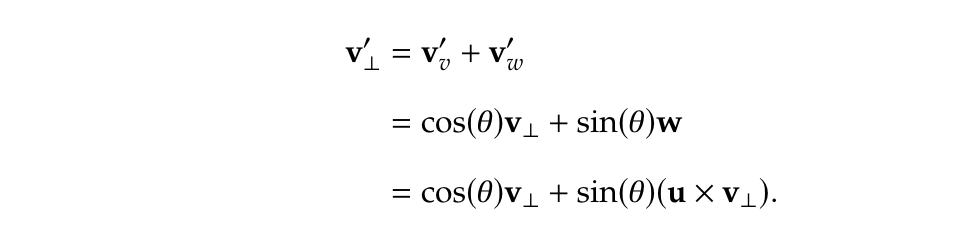
配合平行的分量就是

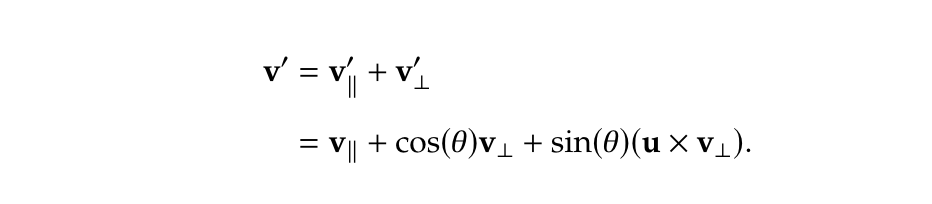
四元数与旋转

我们之前推出过这个公式

四元数的性质告诉我们可以直接将和变成相应的纯四元数

同时我们还可以变换

根据四元数的乘法

可以得到

所以叉乘也能被换成纯四元数（因为它们垂直呢）

𝑣 ′ ⊥ = cos(θ)𝑣⊥ + sin(θ)(𝑢𝑣⊥).

把提出来（四元数满足分配率）

𝑣 ′ ⊥ = cos(θ)𝑣⊥ + sin(θ)(𝑢𝑣⊥) = (cos(θ) + sin(θ)𝑢)𝑣⊥.

就可以发现(cos(θ) + sin(θ)𝑢)也是个四元数

记作

补上平行的分量

𝑣 ′ = 𝑣 ′ ∥ + 𝑣 ′ ⊥ = 𝑣∥ + 𝑞𝑣⊥.

同时还可以直接计算证明两个引理

如此依赖我们可以自定一个四元数

由于pp*（共轭）=1

我们可以把之前的式子变成

𝑣 ′

= 𝑝𝑝∗ 𝑣∥ + 𝑝𝑝𝑣⊥

= 𝑝𝑣∥𝑝 ∗ + 𝑝𝑣⊥𝑝 ∗

= 𝑝(𝑣∥ + 𝑣⊥)𝑝 ∗ .

最后就得到了

看起来这个公式还只是万里征途的第一步，今天就到这里吧