逻辑运算
真值表
没什么好说的
析取 合取 推导
析取就是布尔运算中的或
合取就是布尔运算中的且
推导(蕴含)就是只有10是0,其他是1,等价于
成真赋值 成假赋值
主析取范式DNF 主合取范式CNF
找到所有
嘶为什么呢?我个人猜测,因为CNF就是要求式子满足时为假,所以再在DNF式子外面套一个非,就变成内或外于了
数论
自反、反自反、自反闭包
一个
反之为反自反
将不自反的关系补充为自反,补充后的关系称为原关系的自反闭包
对称、反对称、对称闭包
一个
反之反对称,但是注意反对称并不排斥自反的情况
传递、非传递、传递闭包
一个
否则非传递
常见的关系
偏序:自反,反对称,传递 实数集上的大于等于关系是偏序,但是大于不是,自然数集上的整除关系也是偏序
等价:自反,对称,传递 实数集上的等于关系
相容:自反,对称 集合A={cat, teacher, cold, desk, knife, by},定义关系r = {<x, y> | x, y∈A 且 x和y有相同的字母},那么r是一个相容关系。
关系矩阵
不多说了
复合运算
把传递关系找出来,头尾相接,看清是左复合还是右复合
哈斯图 极值 最值 上确界 下确界
哈斯图的画法要求覆盖性、并且不能有平线、三角性的形成
集合包含关系的哈斯图
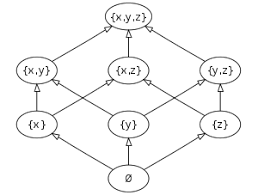
极值可以有多个,最值只能有一个
上确界和最大值的关系:如果最大值存在,那上确界就是最大值,如果不存在,比如
幺元 零元 与逆元
幺元:与其他元素操作后,总是得到其他元素的元素(乘法中的1)
零元:与其他元素操作后,总是的到自己的元素(乘法中的0)
逆元: 对于一个元素,与它操作后得到幺元的元素是逆元(乘法中的倒数)
封闭性 结合性 交换性
对一个集合做操作,不论怎么操作,结果都还在集合内,比如全体整数的加法操作,则满足封闭性,否则不满足,如全体正整数的减法操作
结合性 a*b*c=a*(b*c)
交换性 a*b = b*a
群
一个非空集合
封闭性 结合律 有单位元 每个元都有逆元
证明群也就是证明这四个条件(具体证明得再找个题目)