PCA

Hiton发明的AutoEncoder架构，迅速的取代了PCA

主成分分析是一种常用的无监督学习方法，利用正交变换将线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据，这些线性无关变量被称为主成分，是一种常用的降维方法。

看起来AutoEncoder被更多的用来降维了

直观感受：

对空间中的坐标系进行变换，使得将样本点对变换后的坐标系投影后，方差尽可能的大。

步骤

1. 中心化（目的是令投影后均值为0）

2. 接下来我们要找到一些，使得在方向方差最大

   由于投影后均值也为0，我们可以将投影后的方差表示为

3. 于是我们基于这两个约束求解

   对求导令导数为0，可以得到条件

   此时

4. 基于此我们可以得到

   所谓的方差就是协方差矩阵的特征值，而我们要的向量就是对应特征值的特征向量

5. 降维

   我们可以抛弃较小的特征值，从而实现降维，降维后的信息含量可以计算为

6. 执行PCA变换

例题

pca例题

思考

• 协方差的大小，经过正则化后，是否能表示相关性？

  答案是可以！也就是相关系数r

• 为什么PCA逐渐被AutoEncoder取代？PCA和AutoEncoder二者间的专长在哪里？

  考虑这样一个分布

  

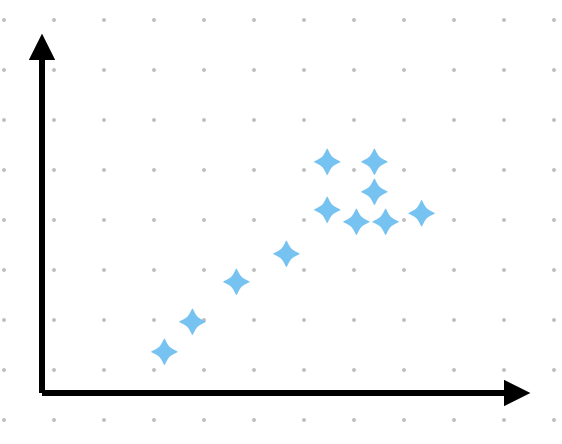
  由于PCA只是对坐标系做线性变换，如果强行降维，右上角的聚簇就难以被区分了，而AutoEncoder并不强行做线性变换，也许可以学到再用一个特征来区分右上角的聚簇。