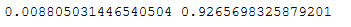累计分布函数 CDF

累计分布函数 F(x) 定义为：

对于离散型随机变量， F(x) 是各个不超过 x 的取值的概率之和：

对于连续型随机变量， F(x) 是从负无穷到 x 的概率密度函数的积分：

概率密度函数 PMF

通过 CDF 计算 PDF

如果 F(x) 是已知的，可以通过求导得到 f(x) ：

十一大分布

1 均匀分布

离散随机变量的均匀分布：假设 X 有 k 个取值：x1, x2, …, xk 则均匀分布的概率密度函数为：

连续随机变量的均匀分布：假设 X 在 [a, b] 上均匀分布，则其概率密度函数为：

2 伯努利分布

伯努利分布：参数为 θ∈[0,1]，设随机变量 X ∈ {0,1}，则概率分布函数为：

期望：

方差：

3 二项分布

假设试验只有两种结果：成功的概率为 θ，失败的概率为 1-θ. 则二项分布描述了：独立重复地进行 n 次试验中，成功 x 次的概率。

概率密度函数：

期望：

方差：

4 高斯分布

正态分布是很多应用中的合理选择。如果某个随机变量取值范围是实数，且对它的概率分布一无所知，通常会假设它服从正态分布。有两个原因支持这一选择：

建模的任务的真实分布通常都确实接近正态分布。中心极限定理表明，多个独立随机变量的和近似正态分布。
在具有相同方差的所有可能的概率分布中，正态分布的熵最大（即不确定性最大）。

典型的一维正态分布的概率密度函数为 :

累计分布函数

${\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\!$

5 拉普拉斯分布

在概率论与统计学中，拉普拉斯分布 (Laplace distribution) 是以皮埃尔-西蒙·拉普拉斯的名字命名的一种连续概率分布。由于它可看作两平移指数分布背靠背拼接在一起，因此又称双指数分布 (Double exponential distribution)。两个相互独立同概率分布指数随机变量之间的差别是按照指数分布的随机时间布朗运动，所以它遵循拉普拉斯分布。

概率密度函数：

期望：

方差：

6 泊松分布

假设已知事件在单位时间（或者单位面积）内发生的平均次数为 λ，则泊松分布描述了：事件在单位时间（或者单位面积）内发生的具体次数为 k 的概率。

概率密度函数：

期望：

方差：

7 指数分布

若事件服从泊松分布，则该事件前后两次发生的时间间隔服从指数分布。由于时间间隔是个浮点数，因此指数分布是连续分布。

概率密度函数：（ t 为时间间隔）

期望：

方差：

8 伽马分布

若事件服从泊松分布，则事件第 i 次发生和第 i+k 次发生的时间间隔为伽玛分布。由于时间间隔是个浮点数，因此伽马分布是连续分布。

概率密度函数：

，

其中， t 为时间间隔，k 称为形状参数， λ 称为尺度参数

期望和方差分别为：

9 贝塔分布

贝塔分布是定义在 (0,1) 之间的连续概率分布。

如果随机变量 X 服从贝塔分布，则其概率密度函数为：

记做

期望为：

方差为：

10 狄拉克分布

狄拉克分布：假设所有的概率都集中在一点 μ上，则对应的概率密度函数为：

其中 δ(.)为狄拉克函数，其性质为：

狄拉克分布的一个典型用途就是定义连续型随机变量的经验分布函数。假设数据集中有样本

则定义经验分布函数：

它就是对每个样本赋予了一个概率质量：

对于离散型随机变量的经验分布，则经验分布函数就是多项式分布，它简单地等于训练集中的经验频率。

经验分布的两个作用：

通过查看训练集样本的经验分布，从而指定该训练集的样本采样的分布（保证采样之后的分布不失真）。
经验分布就是使得训练数据的可能性最大化的概率密度函数。

11 多项式分布与狄里克雷分布

多项式分布的质量密度函数：

狄利克雷分布的概率密度函数：

可以看到，多项式分布与狄里克雷分布的概率密度函数非常相似，区别仅仅在于前面的归一化项：

多项式分布是针对离散型随机变量，通过求和获取概率。
狄里克雷分布时针对连续型随机变量，通过求积分来获取概率。

显著性检验

三、U检验（Z检验）

U检验又称Z检验。

Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法（总体的方差已知）。它是用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著。

Z检验步骤：

第一步：建立虚无假设 H0:μ1 = μ2 ，即先假定两个平均数之间没有显著差异，

第二步：计算统计量Z值，对于不同类型的问题选用不同的统计量计算方法，

1、如果检验一个样本平均数（X）与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为：

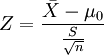
其中：

X是检验样本的均值；

μ0是已知总体的平均数；

S是总体的标准差；

n是样本容量。

2、如果检验来自两个的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著。其Z值计算公式为：

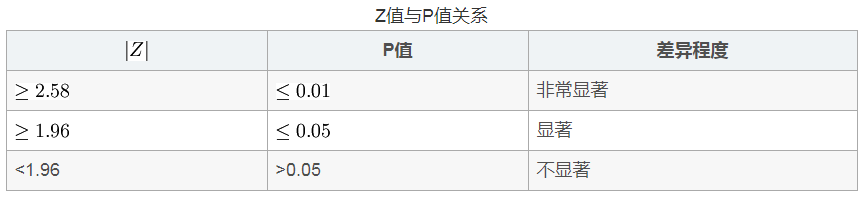
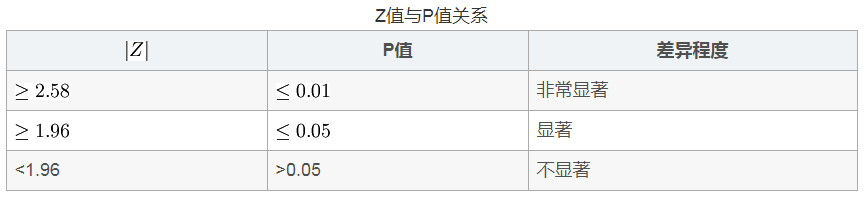
第三步：比较计算所得Z值与理论Z值，推断发生的概率，依据Z值与差异显著性关系表作出判断。如下表所示：

第四步：根据是以上分析，结合具体情况，作出结论。

例子：一种原件，要求使用寿命不低于1000小时，现从一批这种原件中抽取25件，测得其使用寿命的平均值为950小时，已知该原件服从标准差S=100小时的正太分布，试在显著性水平α=0.05下确定这批原件是否合格

解：使用寿命小于1000小时即为不合格，此题为左单侧检验

拒绝域为：Z<-μα ; 查表得 μ0.05=1.65

已知s2=100*2，X=950，n=25 假设H0：μ=1000；H1<1000

选取统计量 Z=（X - μ）（S/√n）= （950-1000）/（100/√25）=-2.5

因为 Z=-2.5<<-μα =-1.65 ，所以拒绝H0，即认为这批原件不合格

四、T检验

亦称student t检验（Student’s t test），主要用于样本含量较小（例如n<30），总体标准差σ未知的正态分布。目的是用来比较样本均数所代表的未知总体均数μ和已知总体均数μ0。

T统计量计算公式：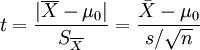

自由度：v=n - 1

T检验的步骤

第一步：建立虚无假设H0:μ1 = μ2，即先假定两个总体平均数之间没有显著差异；

第二步：计算统计量T值，对于不同类型的问题选用不同的统计量计算方法

1、如果要评断一个总体中的小样本平均数与总体平均值之间的差异程度，其统计量T值的计算公式为：

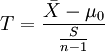
2、如果要评断两组样本平均数之间的差异程度，其统计量T值的计算公式为：

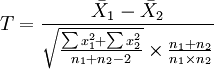
第三步：根据自由度df=n-1，查T值表，找出规定的T理论值并进行比较。理论值差异的显著水平为0.01级或0.05级。不同自由度的显著水平理论值记为T(df)0.01和T(df)0.05

第四步：比较计算得到的t值和理论T值，推断发生的概率，依据下表给出的T值与差异显著性关系表作出判断。

第五步：根据是以上分析，结合具体情况，作出结论。

实际应用中，T检验可分为三种：单样本T检验、配对样本T检验和双独立样本T检验

单样本T检验

例子：已知某班的一次数学测验成绩复查正态分布，现从全班中抽取16人，测得这些人成绩是[50,44,91,90,74,72,89,81,65,62,68,74,63,61,33,47]，问在α=0.05下，是否可以认为全体考生的平均分是70分？

from scipy import stats
import numpy as np
 
rvs = [50,44,91,90,74,72,89,81,65,62,68,74,63,61,33,47]
mean = np.mean(rvs)#均值
std = np.std(rvs)#标准差
print("均值：",mean,"  标准差:",std)
 
t_val, p = stats.ttest_1samp(rvs, 70)
print("t_val:",t_val,"   p值：", p)

结论，因为p值=0.42>0.05，所以可以认为全体考生的平均分是70分

配对样本T检验

配对t检验是采用配对设计方法观察以下几种情形：

1.配对的两个受试对象分别接受两种不同的处理；

2.同一受试对象接受两种不同的处理；

3.同一受试对象处理前后的结果进行比较（即自身配对）；

4.同一对象的两个部位给予不同的处理。

例子：在针织品漂白工艺过程中，要考虑温度对针织品断裂强力（主要质量指标）的影响。为了比较70℃与80℃的影响有无差别，在这两个温度下，分别重复做了8次试验，强力数据如下。问在70℃时的平均断裂强力与80℃时的平均断裂强力间是否有显著差别？假定断裂强力服从正态分布(α=0.05)

70℃时的强力:20.5, 18.8, 19.8, 20.9, 21.5, 19.5, 21.0, 21.2

80℃时的强力:17.7, 20.3, 20.0, 18.8, 19.0, 20.1, 20.0, 19.1

from  scipy.stats import ttest_rel
import pandas as pd
 
x = [20.5, 18.8, 19.8, 20.9, 21.5, 19.5, 21.0, 21.2]
y = [17.7, 20.3, 20.0, 18.8, 19.0, 20.1, 20.0, 19.1]
# 配对样本t检验
t_val, p = ttest_rel(x, y)
print('t_val：',t_val,"   p值：", p)

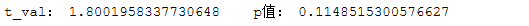
结论: 因为p值=0.1149>0.05, 故接受原假设, 认为在70℃时的平均断裂强力与80℃时的平均断裂强力间无显著差别

双独立样本T检验

例子：甲乙两台机床加工螺丝帽，螺丝帽的半径都服从正态分布，为验证两台机床加工的螺丝帽半径是否相等，分别取两台机床加工的8、7枚螺丝帽进行测量，分别测得[20.5,19.8,19.7,20.4,20.1,20.0,19.0,19.9][20.7,19.8,19.5,20.8,20.4,19.6,20.2] 问两台机器生产的螺丝帽半径是否有差异（α=0.05）

from scipy.stats import norm,ttest_ind #引入正态分布(norm)，T检验（ttest_ind）
 
n1_samples = [20.5,19.8,19.7,20.4,20.1,20.0,19.0,19.9]
n2_samples = [20.7,19.8,19.5,20.8,20.4,19.6,20.2]
 
#独立双样本 t 检验的目的在于判断两组样本之间是否有显著差异：
t_val, p = ttest_ind(n1_samples, n2_samples)
print('t_val：',t_val,"   p值：", p) #p值小于0.05时，认为差异显著；大于等于0.05时表示差异不显著

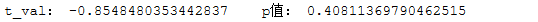
结论：p值=0.408>0.05，接受原假设，甲乙机床制造的螺丝帽半径没有显著性差异

五、卡方检验

卡方检验又称X2检验，就是检验两个变量之间有没有关系。

属于非参数检验，主要是比较两个及两个以上样本率（构成比）以及两个分类变量的关联性分析。根本思想在于比较理论频数和实际频数的吻合程度或者拟合优度问题。

X2计算公式为：

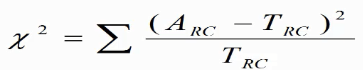
例子1：有AB两种药可以治疗某种疾病，问两种药物的疗效是否相同？

药类	有效	无效	合计	有效率
A药	67	26	93	72.04%
B药	44	30	74	59.46%
合计	111	56	167	66.47%

解：建立假设H0，两种药物疗效相同，计算得其理论值为：

药类	有效	无效	合计
A药	61.8	31.2	93
B药	49.2	24.8	74
合计	111	56	167

X2=（67-61.8）2/61.8+（26-31.2）2/31.2+（44-49.2）2/49.2+（30-24.8）2/24.8=2.94

六、F检验

F检验法是检验两个正态随机变量的总体方差是否相等的一种假设检验方法。

F统计量计算公式：

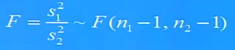
例子：存在两组数据，需要验证这两组数据的方差齐性。
x = [20.5, 18.8, 19.8, 20.9, 21.5, 19.5, 21.0, 21.2]
y = [17.7, 20.3, 20.0, 18.8, 19.0, 20.1, 20.0, 19.1]

from scipy.stats import levene
 
x = [20.5, 18.8, 19.8, 20.9, 21.5, 19.5, 21.0, 21.2]
y = [17.7, 20.3, 20.0, 18.8, 19.0, 20.1, 20.0, 19.1]
f_val, p = levene(x, y)
print(f_val, p)